将节点分为最大组数

4
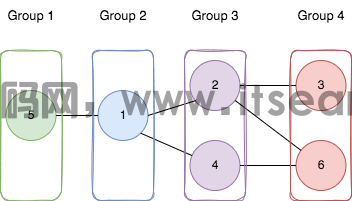
• >说明：
>如图所示：
• >将节点5添加到第一个组。
>将节点1添加到第二组。
• >将节点2和4添加到第三组。
  >将节点3和6添加到第四组。
  • >
  我们可以看到每个边缘都可以满足。
  >可以证明，如果我们创建第五组并将任何节点从第三或第四组移动到其中，那么至少在边缘上都无法满足。
  • >
  • >
  >示例2：
>输入：

>输出：

• >说明：如果将节点1添加到第一个组，将节点2添加到第二组中，然后将节点3添加到第三组以满足前两个边缘，我们可以看到，第三个边缘将不满足第三个边缘。
• 可以证明不可能分组。
• >约束：
  • >
  1

• 1 i
• ，b ⁱ
• a
i
• ！= b_i> 在任何一对顶点之间最多都有一个边缘。
>
• 提示：
• 如果图不是双分，则不可能分组节点。>请注意，我们可以独立解决每个连接的组件的问题，最终答案将只是每个组件中最大组的总数。>

>最后，要解决每个连接的组件的问题，我们可以注意到，如果对于某个节点v，我们将其位置固定在最左边的组中，那么我们也可以评估其他每个节点的位置。该位置是扎根在节点v。

问题，
2. “将节点分为最大组数”
，涉及确定可以将无向图的节点划分为：
3. 的最大组数。

相邻节点的

组成的索引恰好有1个。 如果该图不是双分部分，则不可能进行分组，并且该函数必须返回-1。

>关键点

图形属性：
1. 该图可以断开连接。
>
>验证：

对于每个连接的组件，检查它是否是双分。如果没有，返回-1。

>二分性质：

解决方案涉及bfs以验证双方。

• 联合 - 芬德：有效地分组连接的组件。>
• 方法
预处理：
使用邻接列表表示图形。

>使用union-find来识别连接的组件。

1. bfs验证两肢：>

   对于每个连接的组件，请使用bfs确定它是否为双分。
   如果不是双分，请返回-1。
>计算组计数：

2. 对于每个连接的组件，使用bfs确定最大深度，代表组的最大数量。

   • 组合结果：
   概括所有两部分组件的最大组计数。
>

3. 计划
   构建图形作为邻接列表。
4. >使用union-find对组连接的组件。

   图中每个节点的>：

   >使用bfs检查图形是否是双分部分，并计算该组件的最大深度。
   >作为结果，返回所有组件深度的总和。如果任何组件不是双方，请返回-1。

>让我们在php中实现此解决方案： 2493。将节点划分为最大组数>

当前隐藏内容需要支付

0RNB

已有  人支付

支付查看

购买会员

1、本站目前拥有近 1000+ 精品收费资源，现在加入VIP会员即可全部下载。
2、本资源部分来源其他付费资源平台或互联网收集，如有侵权请联系及时处理。
SEA模板网 » 将节点分为最大组数

欧迪网络科技-sea资源网

分享到：